This morning, a discussion of regression to the mean popped up on Phil's and Tango's blogs. This discussion touches upon some of the recent work I've been doing with Beta distributions, so I figured I'd go ahead and lay out the math linking regression to the mean with Bayesian probability with a Beta prior.
Many of the events we measure in baseball are Bernoulli trials, meaning we simply record whether they happen or not for each opportunity. For example, whether or not a team wins a game, or whether or not a batter gets on base are Bernoulli trials. When we observe these events over a period of time, the results follow a binomial distribution.
When we observe these binomial events, each team or player has a certain amount of skill in producing successes. Said skill level will vary from team to team or player to player, and, as a result, we will observe different results from different teams or players. Albert Pujols, for example, has a high degree of skill at getting on base compared to the whole population of MLB hitters, and we would expect to observe him getting on base more often than, say, Emilio Bonifacio.
The variance in talent levels is not the only thing driving the variance in obvserved results, however. As with any binomial process (excepting those with 0% or 100% probabilities, anyway), there is also random variance as described by the binonial distribution. Even if Albert's on-base skill is roughly 40%, and Bonifacio's is roughly 33%, it is still possible that you will occasionally observe Emilio to have a higher OBP than Albert over a given period of time.
In baseball, it is a practical problem that we do not know the true probability linked to each team's or player's skill, only their observed rate of success. Thus, if we want to know the true talent probability, we have to estimate it from the observed.
One way to do this is with regression to the mean. Say that we have a player with a .400 observed OBP over 500 PAs, and we want to estimate his true talent OBP. Regression to the mean says we need to find out how much, on average, our observed sample will reflect the hitter's true talent OBP, and how much it will reflect random binomial variation. Then, that will tell us how many PAs of the league average we need to add to the observed performance to estimate the hitter's true talent.
For example, say we decide that the number of league average PAs we need to add to regress a 500 PA sample of OBP is 250. We would take the observed performance (200 times on base in 500 PAs), and add 82.5 times on base in 250 PAs (i.e. the league average performance, assuming league average is about .330) to that.
200+82.5......282.5
------------ = -------- = .377
500+250........750
Therefore, regression to the mean would estimate the hitter's true OBP talent at .377.
As Phil demonstrated, once you decide that you have to add 250 PAs of league average performance to your sample to regress, you would use that same 250 PA figure to regress any OBP performance, regardless of how many PAs are in the observed sample. Whether you have 10 observed PAs or 1000 observed PAs, the amount of average performance you have to add to regress does not change.
Now, how would one go about finding that 250 PA figure? One way is to figure out the number of PAs at which the random binomial variance is equal to the variance of true talent in the population.
Start by taking the observed variance in the population. You would look at all hitters over a certain number of PAs (say, 500, for example), and you might observe that the variance in their observed OBPs is about .00132, with the average about .330. The observed variance is equal to the sum of the random binomial variance and the variance of true OBP talent across the population of hitters. We don't know the variance of true talent, but we can calculate the random binomial variance as p(1-p)/n, where p is the probability of getting on base (.330 for our observed population) and n is the observed number of PAs (500 in this case). For this example, that would be about .00044. Therefore, the variance of true talent in the population is approximately:
.00132 - .00044 = .00088
Next, we find the number of PAs where the random binomial variance will equal the variance of true talent:
p*(1-p)/n = true_var
.330*(1-.330)/n = .00088
n = .330*(1-.330)/.00088 ≈ 250
We can also approach the problem of estimating true talent from observed performance using Bayesian probability. In order to use Bayes, we need to make an assumption about the distribution of true talent in the population the hitter is being drawn from (i.e. the prior distribution). We will assume that true talent follows a Beta distribution.
Return now to our .400 observed OBP example. Bayes says the posterior distribution (i.e. the distribution of possible true talents for a hitter drawn from the prior distribution after observing his performance) is proportional to the product of the prior distribution and the likelihood function (i.e. the binomial distribution, which is the likelihood of observing a each possible OBP, given the prior probability).
The prior Beta distribtuion is:
x^(α-1) * (1-x)^(β-1)
------------------------
..........B(α,β)
where B(α,β) is a constant equal to the Beta function with parameters α and β.
The binomial likelihood for observing s successes in n trials (i.e. the observed on-base performance) is:
.....n!
--------- * x^s * (1-x)^(n-s)
s!(n-s)!
where x is the true probability of a success.
Next, we multiply the prior distribution by the likelihood distribution:
x^(α-1) * (1-x)^(β-1) .........n!
------------------------- * --------- * x^s * (1-x)^(n-s)
............B(α,β).... .......... s!(n-s)!
combine the exponents for the x and (1-x) factors:
x^(α + s - 1) * (1-x)^(β + n - s - 1).. .....n!
--------------------------------------- * --------
.......................B(α,β) ...................... s!(n-s)!
Separating the constant factors from the variables:
...........n!
------------------- * x^(α + s - 1) * (1-x)^(β + n - s - 1)
s!(n-s)! * B(α,β)
This product is proportional to the posterior distribution, so the posterior distribution will be the above multiplied by some constant in order to scale it so that the cumulative probability equals one. Since the left portion of the above expression is already a constant, we can simply absorb that into the scaling constant, and the final posterior distribution then becomes:
C * x^(α + s - 1) * (1-x)^(β + n - s - 1)
Notice that the above distribution conforms to a new Beta distribution with parameters α+s and β+n-s, and with a constant C = 1/B(α+s,β+n-s). When the prior distribution is a Beta distribution with parameters α and β and the likelihood function is binomial, then the posterior distribution will also be a Beta distribution, and it will have the parameters α+s and β+n-s.
We still need to choose values for the parameters α and β for the prior distribution. Recall from the regression example that we found a mean of .330 and a variance of .00088 for the true talent in the population (i.e. the prior distribution), so we will choose values for α and β that give us those values. For a Beta distribution, the mean is equal to:
α/(α+β)
and the variance is equal to:
............αβ
----------------------
(α+β)^2 * (α+β+1)
A bit of algebra gives us values for α and β of approximately 82.5 and 167.5 respectively. That means the posterior distribution will have as parameters:
α+s = 82.5 + 200 = 282.5
β+n-s = 167.5 + 500 - 200 = 467.5
and a mean of
........282.5...........282.5
----------------- = ------- = .377
282.5 + 467.5.......750
As you can see, this is identical to the regression estimate. This will always be the case as long as the prior distribution is Beta and the likelihood is binomial. We can see why if we derive the regression constant (the number of PAs of league average we need to add to the observed performance in order to regress) from the prior distribution.
Recall that the regression constant can be found by finding the point where random binomial variance equals prior distribution variance. Therefore:
p(1-p)/k ≈ prior variance
where k is the regression constant and p is the population mean.
p(1-p)/k ≈ αβ / ( (α + β)^2(α + β + 1) ) ; p ≈ α/(α+β)
α/(α+β) * ( 1 - α/(α+β) ) / k . ≈ αβ / ( (α + β)^2 * (α + β + 1) )
α/(α+β) - α^2/(α+β)^2.........≈ k * αβ / ( (α + β)^2 * (α + β + 1) )
(α(α+β) - α^2)/(α+β)^2 ...... ≈ k * αβ / ( (α + β)^2 * (α + β + 1) )
(α(α+β) -α^2)....................... ≈ k * αβ / (α + β + 1)
(α^2 + αβ - α^2) ..................≈ k * αβ / (α + β + 1)
αβ.......................................... ≈ k * αβ / (α + β + 1)
1 .............................................≈ k / (α + β + 1)
k....................,,,,,,,,,,,,,,,,........ ≈ α + β + 1
Since α and β for the prior in our example are 82.5 and 167.5, k would be 82.5 + 167.5 + 1 = 251.
This estimate of k is actually biased, because it assumes a random binomial variance based only on the population mean, whereas the actual random binomial variance for the prior distribution will be the average binomial variance over the entire distribution. In other words, not all of the population will have a .330 OBP skill; some hitters will have a .300 skill, while others will have a .400 skill, and they will all have different binomial variances associated with them. More precisely, the random binomial variation for the prior distribution will be the following definite integral taken from 0 to 1:
⌠ x(1-x)
| ------- * B(x;α,β) dx
⌡...k
which, conceptually, is the weighted sum of the the binomial variances for each possible value from the prior distribution, where each binomial variance is weighted by the probability density function of the prior.
.......1........ ⌠
------------ | x(1-x) * x^(α-1) * (1-x)^(β-1) dx
k * B(α,β) ⌡
........1....... ⌠
------------ | x^α * (1-x)^β dx
k * B(α,β) ⌡
The definite integral is in the form of the Beta function B(α+1,β+1), so we can rewrite this as
B(α+1,β+1)
-------------
k * B(α,β)
The Beta function is interchangeable with the Gamma Function in the following manner:
B(α,β) = Γ(α)*Γ(β) / Γ(α+β)
replacing the two Beta functions with their Gamma equivalencies:
Γ(α+1) * Γ(β+1) * Γ(α+β)
-------------------------------
k * Γ(α) * Γ(β) * Γ(α+β+2)
This revision is useful because the Gamma function has a property where Γ(x+1)/Γ(x) = x, so the above reduces to:
αβ * Γ(α+β)
---------------
k * Γ(α+β+2)
Furthermore, since Γ(x+1)/Γ(x) = x, it follows that Γ(x+2)/Γ(x+1) = x+1. If we multiply those two equations together, we find that
Γ(x+1)....Γ(x+2)
-------- * -------- = x(x+1)
..Γ(x)......Γ(x+1)
Γ(x+2)/Γ(x) = x(x+1)
Γ(x)/Γ(x+2) = 1/(x(x+1))
Therefore
.αβ * Γ(α+β) ..................αβ
---------------- = ------------------------
k * Γ(α+β+2).....k * (α+β) * (α+β+1)
Now that we have a manageable expression for the random binomial variance of the prior distribution, we return to the requirement that random binomial variance equals the variance of the prior distribution:
..............αβ ................................αβ
------------------------ = -----------------------
k * (α+β) * (α+β+1)......(α+β)^2 * (α+β+1)
k * (α+β) * (α+β+1) = (α+β)^2 * (α+β+1)
k = α+β
Using a more precise calculation for the random binomial variance of the prior, we find that k = α+β rather than α+β+1. Note that when we estimate k by assuming a constant binomial variance of p(1-p)/k, we get a value of k exactly 1 higher than when we run the full calculation for the binomial variance. This is useful because the former calculation is much simpler than the latter, so we can calculate k by using the former method and then subtracting 1. Also note that the 250 value we got in the initial regression to the mean example would also be 1 too high if we were using more precise figures; I've just been rounding them off for cleanliness' sake.
Let's look now at the calculation for regression to the mean:
true talent estimate = (s+pk)/(n+k)
where s is the observed successes, n is the observed trials, p is the population mean, and k is the regression constant.
We know from our prior that p=α/(α+β) and k=α+β, so
(s+pk)/(n+k) =
s + (α+β)*α/(α+β)
----------------------
......n + α + β
...α + s
-----------
α + β + n
And what does Bayes say? Our posterior is a Beta with parameters α+s and β+n-s, which has a mean
.......(α+s)
-----------------
(α+s)+(β+n-s)
...α + s
-----------
α + β + n
So Bayes and regression to the mean produce identical talent estimates under these conditions (a binomial process where true talent follows a Beta distribution).
k is far easier to estimate directly (such as by using the method in the initial regression tot he mean example) than α and β, so we would typically calculate α and β from k. To do that, we use the fact that p = α/(α+β), and that k=α+β, so by substitution we can easily find that:
α=kp
β=k(1-p)
where k is the regression constant and p is the population mean.
We can also see that the regression amount will be constant regardless of the number of observed PAs, because when we take our Bayesian talent estimate:
...α + s
-----------
α + β + n
we see that we are always adding the quantity kp (as substituted for α) to the observed successes (s), and always adding the quantity k (as substituted for (α+β)) to the observed trials (n), no matter what observed values we have for s and n. The amounts we add to the observed successes and trials depend only on the parameters of the prior, which do not change.
Continue Reading...
Regression to the Mean and Beta Distributions
Posted by
Kincaid
on Wednesday, August 17, 2011
/
Labels:
Bayes,
beta distribution,
regression to the mean
/
Comments: (0)
Poisson Processes in Sports
In sports, the problem of relating a team's offensive and defensive production to its W-L record is closely related to the distribution of scoring events in the sport. For example, say you want to know how often a team that scores, on average, 4 times per game and allows 3 scores per game is expected to win. It is not enough to simply know that the team averages 4 scores and 3 scores allowed; you also have to have an idea of how likely the team is to score (or allow) 0 times, 1 time, 2 times, etc. If the nature of the sport provides for a very tight range of scores for each team (i.e. the 4-score team is very unlikely to score 0 or 1 time, or 7 or 8 times), then the team will win more often than if the sport sees a wider distribution of observed scores for each team.
Let's say, for example, that the team in this example scores and allows scores in the following distribution:
In the above table, the team would score 0 times 6% of the time and allow 0 scores 14% of the time.
To find the chances of the team winning, you first figure its chances of outscoring its opponents when it scores once. Since this team will allow fewer than one score 14% of the time, it would be expected to win 14% of the time it scores once. The team scores once 10% of the time, so one-score victories should account for .1*.14=1.4% of its games. Continuing for 2-score victories, the team allows less than 2 scores 29% of the time (14%+15%), so 2-score victories account for .13 2-score games * .29 wins per 2-score game = 3.8% of the team's total games.
Doing this for each possible number of scores, the team will win a total of 56% of its games. Repeating the same process for losses, it will lose 32% of the time (the other 12% of games will end tied).
As long as we know the probability of each possible number of scores and scores allowed, the expected W-L performance can be found in this way. In terms of summation notation, it looks something like this:
..∞............ i-1
∑ps(i) ∑pa(j)
i=0......,..j=0
where ps(i) is the probability of scoring i number of times and pa(j) is the probability of allowing j number of scores.
This is only useful if you have a reasonable model for finding these probabilities, however, which requires you to have some model for the distribution of possible scores around the team average. In baseball, no such distribution is obvious, so instead of the above process, we use shortcuts like PythagenPat to model the results of translating the underlying distribution of possible run-totals to an expected win percentage (by the way, the above example roughly resembles the actual distribution for a baseball team; traditional pythag would give you 4^2/(4^2+3^2) = 16/25 = .640 w%, while the example (ignoring ties) shows .56W/(.56W+.32L) = .636). Steven Miller showed that a Weibull distribution of runs gives a Pythagorean estimate of W%, and that the Weibull distribution is a reasonable assumption for his sample data (the 2004 American League), but that is just working backwards from the model in place.
Some sports, however, do present an obvious choice of model, namely the Poisson distribution. Both soccer and hockey are decent examples of Poisson processes because
-play happens over a predetermined length, measured in a continuous fashion (i.e. time, as opposed to something like baseball which is measured in discreet units of outs or innings)
-goals can only come one at a time (as opposed to something like basketball, where points can come in groups of 1, 2, 3, or 4)
-the number of goals scored over a given period of the game is largely independent of the number of goals scored over a separate period of the game (the fluid nature of possession is a key attribute here; for a sport like American football where a score dictates who has possession for a significant chunk of time, a team's score over one five-minute span will be somewhat dependent on whether it scored in the previous five-minute span, for example)
-the expectation for the number of goals over a period of time (once you know who is playing) depends mostly on the length of time
Hockey has at least one exception to the requirements of a Poisson process, in that the number of goals scored at the end of the game is not always independent of the number of goals scored earlier in the game due to empty net goals, but I don't know how much of an issue this presents. Soccer is a more straight-forward example (as well as a more homogeneous example due to the relative lack of substitution and penalties that are continually affecting the score-rate in hockey). Both, however, generally fit the mould for a Poisson process.
Using a Poisson distribution to fill out a table as in the above example (if you have Excel or a similar spreadsheet program, it should have a Poisson distribution function built in), we can then calculate expected W-L performances for a team. The first and second columns use the average number of goals for and against , respectively, as λ (in Excel, Poisson.Dist(x,avg goals for/against,False), where x is 1,2,3..). Say we do this for a soccer team that we expect to score an average of 2 goals per game and allow an average of 1 goal per game against its opponent. We get the following probabilities:
W: .606
L: .183
D: .212
Using the traditional soccer point-format (3 points for a win, 1 for a draw), this team would average about 2.03 points per game against its opponent.
We can also use the Poisson distribution to figure out what to expect if the game goes to overtime. Elimination soccer matches typically have a 30 minute OT (two 15-minute periods), so the λ (which, recall, are the average goals for and against, which are 2 and 1 in this example) for the OT will be 1/3 their regulation-match value (note that finding λ for regular-season hockey OTs will be more complicated because the 4v4 format will affect the scoring rate). Reconstructing the table with λ values of 2/3 and 1/3, we get the following results for games that go to OT:
OTW: .384
OTL: .161
OTD: .454
If overtime ends in a draw, the game is usually decided on PKs. If we assume that each team is 50/50 to win in PKs (which is not necessarily the case, but shootout odds should be closer to 50/50 than the rest of the match, and the odds in a shootout aren't necessarily based on expected goals for and against for the match), then our team's expected win% once a game goes to OT is .384 + .5*.454 = .611. Remember that the team wins 60.6% of the time in regulation, and the game goes to OT 21.2% of the time, so the team's total expected wins is .606 + .611*.212 = .735.
If we want to model a sudden death OT, such as in the Stanley Cup playoffs, the odds of winning in regulation remain unchanged, but we have to use a different formula to determine the chances of winning once the game goes to overtime. The Poisson distribution works for estimating the probability of scoring a certain number of goals in a pre-determined amount of time (such as a 20-minute period or a 60-minute game), but not for estimating the time until the next goal. For that, we instead need the exponential distribution, which models the amount of time until the next goal.
We want to know the probability that our team's time until its next goal is less than its opponent's time to its next goal. Recall the above formula we used to determine the odds of our team's goals scored being higher than its opponent's:
..∞............ i-1
∑ps(i) ∑pa(j)
i=0......,..j=0
Here, we use something similar, except that we want to know the chances of our team's value (time to the next goal) is less than that of its opponenent:
..∞............ i-1
∑pa(i) ∑ps(j)
i=0......,..j=0
where ps(j) is the probability of our team's next goal coming after j amount of elapsed time, and pa(i) is the probability of its opponent's next goal coming after i amount of elapsed time.
Additionally, we are now dealing with a continuous variable (time elapsed) rather than a discreet variable (number of goals scored), so we need to integrate instead of summate:
⌠∞.........⌠x
⌡0 f(x) ⌡0 g(x) dx dx
where f(x) models the amount of time until the opponent's next goal, and g(x) models the amount of time until our team's next goal. In this formula, f(x) is an exponential probability density function with λ=expected goals allowed (Ga), and ∫g(x)dx is an exponential cumulative distribution function with λ=expected goals scored (Gs):
⌠∞
⌡0 Ga*e^-(Gax)*(1-e^-(Gsx)) dx
This might look a bit ugly (or maybe not since e^x is such a simple integration), but it simplifies to just:
...Gs
-------
Gs+Ga
This makes perfect sense if we think about the next goal being a goal randomly selected from the distribution of possible goals in the game: the odds that the randomly selected goal comes from our team equal the percentage of total goals we expect to come from our team, and the odds that the randomly selected goal comes from our opponent equal the percentage of total goals we expect to come from them.
Now that we have a model for sudden-death OT, we can estimate a team's chances of winning a game with sudden death OT. For example, say we have a hockey game where we expect our team to score 3 goals and allow 2 goals on average. This team would be expected to win in regulation about 58.5% of the time, lose in regulation about 24.7% of the time, and go to OT 16.8% of the time. Once in OT, it will win 3/(3+2)=60% of the time, so its total expected wins is .585 + .6*.168 = .686.
Another interesting use of these distributions is to evaluate different strategies or lineups for a team (given that you can estimate the expected goals scored and allowed for varying lineups/strategies). Returning to the soccer team example where we have a team that we expect to score two goals and allow one, let's say that they are capable of making adjustments that make them stronger defensively, but at the cost of a significant portion of their offense. Say that they can play a defensive game and allow just .38 goals per game, but that doing so reduces their expected offensive output to 1.2 goals per game. In regular league play, the new defensive alignment will still average 2.03 points per game, so there is no benefit to this change.
In a tournament elimination game, however, their win expectancy rises from .735 to .761, because the increase in regulation draws will still lead to a lot of wins (~61% of OT games) instead of just 1-point outcomes. What's more, if they switch back to the more aggressive game in OT (their 2 goals for, 1 goal against form), they can slightly improve their OT win odds (from .608 to .611) by avoiding more shootouts.
Similarly, a sudden death format, where only the ratio of goals scored to goals allowed matters, can also produce different ideal strategies. Doubling both expected goals scored and allowed, for example, would have a significant effect on a team's odds of winning in regulation, but would have no effect on sudden-death because it preserves the ratio of offense to defense, and changes that have no impact on regulation (like going from 2 goals for/1 goal against to 1.2 goals for/.38 goals against in a regular season format soccer match) could have a significant impact on sudden death chances (.667 to .759 once you get to sudden death). Of course, any changes in strategy called for by different formats would depend on the team's ability to adapt to a different style of play and on how such changes affect its expected offensive and defensive production, but it is possible for an ideal lineup or strategy in one format to not be ideal in another, and using Poisson distributions to find the connection between offensive and defensive production and expected W-L performance is helpful in evaluating potential changes.
Continue Reading...
Let's say, for example, that the team in this example scores and allows scores in the following distribution:
| score | allow | |
| 0 | 0.06 | 0.14 |
| 1 | 0.1 | 0.15 |
| 2 | 0.13 | 0.17 |
| 3 | 0.15 | 0.17 |
| 4 | 0.17 | 0.12 |
| 5 | 0.13 | 0.1 |
| 6 | 0.1 | 0.07 |
| 7 | 0.07 | 0.04 |
| 8 | 0.05 | 0.03 |
| 9 | 0.03 | 0.01 |
| 10 | 0.01 | 0 |
In the above table, the team would score 0 times 6% of the time and allow 0 scores 14% of the time.
To find the chances of the team winning, you first figure its chances of outscoring its opponents when it scores once. Since this team will allow fewer than one score 14% of the time, it would be expected to win 14% of the time it scores once. The team scores once 10% of the time, so one-score victories should account for .1*.14=1.4% of its games. Continuing for 2-score victories, the team allows less than 2 scores 29% of the time (14%+15%), so 2-score victories account for .13 2-score games * .29 wins per 2-score game = 3.8% of the team's total games.
Doing this for each possible number of scores, the team will win a total of 56% of its games. Repeating the same process for losses, it will lose 32% of the time (the other 12% of games will end tied).
As long as we know the probability of each possible number of scores and scores allowed, the expected W-L performance can be found in this way. In terms of summation notation, it looks something like this:
..∞............ i-1
∑ps(i) ∑pa(j)
i=0......,..j=0
where ps(i) is the probability of scoring i number of times and pa(j) is the probability of allowing j number of scores.
This is only useful if you have a reasonable model for finding these probabilities, however, which requires you to have some model for the distribution of possible scores around the team average. In baseball, no such distribution is obvious, so instead of the above process, we use shortcuts like PythagenPat to model the results of translating the underlying distribution of possible run-totals to an expected win percentage (by the way, the above example roughly resembles the actual distribution for a baseball team; traditional pythag would give you 4^2/(4^2+3^2) = 16/25 = .640 w%, while the example (ignoring ties) shows .56W/(.56W+.32L) = .636). Steven Miller showed that a Weibull distribution of runs gives a Pythagorean estimate of W%, and that the Weibull distribution is a reasonable assumption for his sample data (the 2004 American League), but that is just working backwards from the model in place.
Some sports, however, do present an obvious choice of model, namely the Poisson distribution. Both soccer and hockey are decent examples of Poisson processes because
-play happens over a predetermined length, measured in a continuous fashion (i.e. time, as opposed to something like baseball which is measured in discreet units of outs or innings)
-goals can only come one at a time (as opposed to something like basketball, where points can come in groups of 1, 2, 3, or 4)
-the number of goals scored over a given period of the game is largely independent of the number of goals scored over a separate period of the game (the fluid nature of possession is a key attribute here; for a sport like American football where a score dictates who has possession for a significant chunk of time, a team's score over one five-minute span will be somewhat dependent on whether it scored in the previous five-minute span, for example)
-the expectation for the number of goals over a period of time (once you know who is playing) depends mostly on the length of time
Hockey has at least one exception to the requirements of a Poisson process, in that the number of goals scored at the end of the game is not always independent of the number of goals scored earlier in the game due to empty net goals, but I don't know how much of an issue this presents. Soccer is a more straight-forward example (as well as a more homogeneous example due to the relative lack of substitution and penalties that are continually affecting the score-rate in hockey). Both, however, generally fit the mould for a Poisson process.
Using a Poisson distribution to fill out a table as in the above example (if you have Excel or a similar spreadsheet program, it should have a Poisson distribution function built in), we can then calculate expected W-L performances for a team. The first and second columns use the average number of goals for and against , respectively, as λ (in Excel, Poisson.Dist(x,avg goals for/against,False), where x is 1,2,3..). Say we do this for a soccer team that we expect to score an average of 2 goals per game and allow an average of 1 goal per game against its opponent. We get the following probabilities:
W: .606
L: .183
D: .212
Using the traditional soccer point-format (3 points for a win, 1 for a draw), this team would average about 2.03 points per game against its opponent.
We can also use the Poisson distribution to figure out what to expect if the game goes to overtime. Elimination soccer matches typically have a 30 minute OT (two 15-minute periods), so the λ (which, recall, are the average goals for and against, which are 2 and 1 in this example) for the OT will be 1/3 their regulation-match value (note that finding λ for regular-season hockey OTs will be more complicated because the 4v4 format will affect the scoring rate). Reconstructing the table with λ values of 2/3 and 1/3, we get the following results for games that go to OT:
OTW: .384
OTL: .161
OTD: .454
If overtime ends in a draw, the game is usually decided on PKs. If we assume that each team is 50/50 to win in PKs (which is not necessarily the case, but shootout odds should be closer to 50/50 than the rest of the match, and the odds in a shootout aren't necessarily based on expected goals for and against for the match), then our team's expected win% once a game goes to OT is .384 + .5*.454 = .611. Remember that the team wins 60.6% of the time in regulation, and the game goes to OT 21.2% of the time, so the team's total expected wins is .606 + .611*.212 = .735.
If we want to model a sudden death OT, such as in the Stanley Cup playoffs, the odds of winning in regulation remain unchanged, but we have to use a different formula to determine the chances of winning once the game goes to overtime. The Poisson distribution works for estimating the probability of scoring a certain number of goals in a pre-determined amount of time (such as a 20-minute period or a 60-minute game), but not for estimating the time until the next goal. For that, we instead need the exponential distribution, which models the amount of time until the next goal.
We want to know the probability that our team's time until its next goal is less than its opponent's time to its next goal. Recall the above formula we used to determine the odds of our team's goals scored being higher than its opponent's:
..∞............ i-1
∑ps(i) ∑pa(j)
i=0......,..j=0
Here, we use something similar, except that we want to know the chances of our team's value (time to the next goal) is less than that of its opponenent:
..∞............ i-1
∑pa(i) ∑ps(j)
i=0......,..j=0
where ps(j) is the probability of our team's next goal coming after j amount of elapsed time, and pa(i) is the probability of its opponent's next goal coming after i amount of elapsed time.
Additionally, we are now dealing with a continuous variable (time elapsed) rather than a discreet variable (number of goals scored), so we need to integrate instead of summate:
⌠∞.........⌠x
⌡0 f(x) ⌡0 g(x) dx dx
where f(x) models the amount of time until the opponent's next goal, and g(x) models the amount of time until our team's next goal. In this formula, f(x) is an exponential probability density function with λ=expected goals allowed (Ga), and ∫g(x)dx is an exponential cumulative distribution function with λ=expected goals scored (Gs):
⌠∞
⌡0 Ga*e^-(Gax)*(1-e^-(Gsx)) dx
This might look a bit ugly (or maybe not since e^x is such a simple integration), but it simplifies to just:
...Gs
-------
Gs+Ga
This makes perfect sense if we think about the next goal being a goal randomly selected from the distribution of possible goals in the game: the odds that the randomly selected goal comes from our team equal the percentage of total goals we expect to come from our team, and the odds that the randomly selected goal comes from our opponent equal the percentage of total goals we expect to come from them.
Now that we have a model for sudden-death OT, we can estimate a team's chances of winning a game with sudden death OT. For example, say we have a hockey game where we expect our team to score 3 goals and allow 2 goals on average. This team would be expected to win in regulation about 58.5% of the time, lose in regulation about 24.7% of the time, and go to OT 16.8% of the time. Once in OT, it will win 3/(3+2)=60% of the time, so its total expected wins is .585 + .6*.168 = .686.
Another interesting use of these distributions is to evaluate different strategies or lineups for a team (given that you can estimate the expected goals scored and allowed for varying lineups/strategies). Returning to the soccer team example where we have a team that we expect to score two goals and allow one, let's say that they are capable of making adjustments that make them stronger defensively, but at the cost of a significant portion of their offense. Say that they can play a defensive game and allow just .38 goals per game, but that doing so reduces their expected offensive output to 1.2 goals per game. In regular league play, the new defensive alignment will still average 2.03 points per game, so there is no benefit to this change.
In a tournament elimination game, however, their win expectancy rises from .735 to .761, because the increase in regulation draws will still lead to a lot of wins (~61% of OT games) instead of just 1-point outcomes. What's more, if they switch back to the more aggressive game in OT (their 2 goals for, 1 goal against form), they can slightly improve their OT win odds (from .608 to .611) by avoiding more shootouts.
Similarly, a sudden death format, where only the ratio of goals scored to goals allowed matters, can also produce different ideal strategies. Doubling both expected goals scored and allowed, for example, would have a significant effect on a team's odds of winning in regulation, but would have no effect on sudden-death because it preserves the ratio of offense to defense, and changes that have no impact on regulation (like going from 2 goals for/1 goal against to 1.2 goals for/.38 goals against in a regular season format soccer match) could have a significant impact on sudden death chances (.667 to .759 once you get to sudden death). Of course, any changes in strategy called for by different formats would depend on the team's ability to adapt to a different style of play and on how such changes affect its expected offensive and defensive production, but it is possible for an ideal lineup or strategy in one format to not be ideal in another, and using Poisson distributions to find the connection between offensive and defensive production and expected W-L performance is helpful in evaluating potential changes.
Continue Reading...
Luis Gonzalez painting
Posted by
Kincaid
on Sunday, May 15, 2011
/
Labels:
2001 World Series,
Game 7,
Luis Gonzalez,
Mariano Rivera
/
Comments: (1)
My most recent painting, for a charity auction in Phoenix, AZ. It's supposed to be Game 7 of the 2001 World Series, but, coincidentally, it also happens to feature the only two numbers retired by the Diamondbacks. Click the image for a larger size.
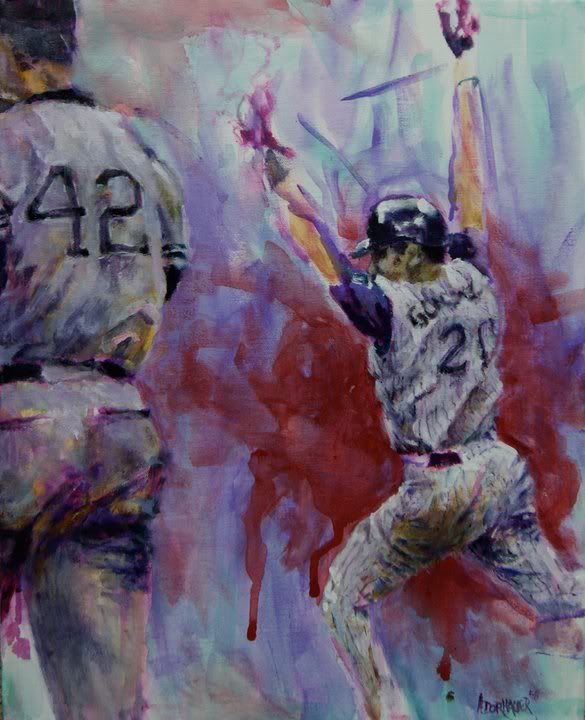
Continue Reading...
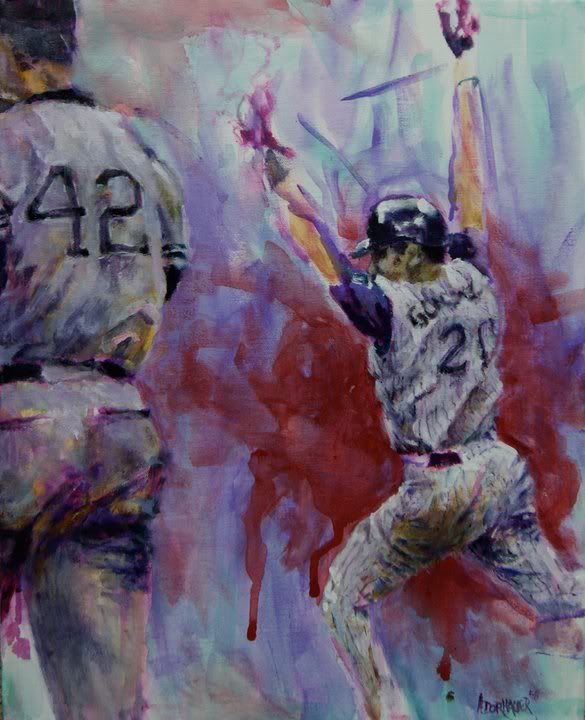
Continue Reading...
Bayes, Regression, and the Red Sox (but mostly Bayes)
WARNING: Math heavy post.
Let's say that we have a hypothetical Major League team that has started the season 2-10. Say we want to see how likely it is that a team that goes 2-10 is still a .500 team. If you've taken any statistics courses, you may be familiar with hypothesis testing where you formulate a null hypothesis that the team is a .500 team, and then calculate the probability that they would go 2-10 by chance. You would then see that a .500 team will go 2-10 (or worse) over a 12 game span less than 2% of the time, and you'd probably reject your null hypothesis, depending on how high you set your significance level.
This does not, however, tell you anything about the likelihood that the team actually is a .500 team, only the likelihood that they would perform that badly if they were in fact a .500 team. To address the former issue, we can instead use a Bayesian approach.
To do that, we have to make an assumption about the population that the team is drawn from (in other words, about the spread of talent across all teams in the league). Most teams in MLB fall somewhere in the .400-.600 range (at least in true talent, if not in observed win percentage), so for convenience sake, let's just assume MLB teams follow a normal distribution of talent with a standard deviation of .050 W%.
This is our prior distribution. Once we have that, we can apply Bayes' Theorem:
P(A|B) = P(B|A)*P(A)/P(B)
We want to find the probability of A given B [P(A|B)], which is to say that we want to find the probability that a team drawn from our prior population distribution (u=.500, SD=.050) is actually a .500 (or better) team, given that we have observed that team to go 2-10 over 12 games. To do this, we need to find the probabilities P(B|A), P(A), and P(B).
P(A) is the simplest. This is the probability of a random team drawn from our prior distribution is at least a .500 team, ignoring of what we observed over the 12 game sample. This is just .500, because the population is centered around .500. So, P(A)=.5.
*NOTE-if you want to use a W% other than .500, all you have to do is find the probability of drawing a W% at least that high from the prior distribution, which is trivial when the prior distribution is normal since that is a common computer function. If you don't have a program that can calculate normal distribution probabilities, you can use an online tool.
P(B) is a bit more difficult. This is the probability that we observe a random team drawn from our prior distribution to go 2-10 over 12 games. This would be simple to calculate for any one team if we already know its true W%, but we need to know the average probability for all possible teams we could draw from our prior distribution. This will require a bit of calculus.
For any one team with a known true W% (p), the probability of going 2-10 is:
( 12! / (2! * 10!) ) * p^2 * (1-p)^10
where 12 represents the number of total games, 2 the number of wins, and 10 the number of losses. We need to find the average value of that formula across the entire prior distribution.
To do this, we utilize the same principle as a weighted average. In this case, the weight given to each possible value of p is represented by the probability density function of the prior distribution. So, for example, the odds of a .400 team going 2-10 are about 6.4%, and that 6.4% gets weighted by the quantity f(p), where f(p) is the pdf for our prior normal distribution. We repeat this for each possible value of p, add up the weighted terms, and then divide by the sum of the weights. As you have probably guessed, this means taking the definite integral (from p=0 to p=1) of the probabilities weighted by f(p):
INTEGRAL(f(p) * ( ( 12! / (2! * 10!) ) * p^2 * (1-p)^10 ) dp)
f(p) is just the normal distribution pdf, which is:
f(p) = e^((-((x-u)^2))/(2*VAR))/(sqrt(2*Pi*VAR)) ; u=.5, VAR=.05^2=.0025
As fun as it sounds to go ahead and do that by hand, we'll just let computers do this part for us too, using an online definite integral calculator. You can copy and paste this into the function field if you want to try it for yourself:
((12!/(2!*10!))*exp((-((x-.5)^2))/(2*.0025))*(x^2*(1-x)^10)/(sqrt(2*3.14159*.0025)))
or, more generally, if you want to play around with different records or different means and variances for the prior normal distribution:
(((W+L)!/(W!*L!))*exp((-((x-u)^2))/(2*VAR))*(x^W*(1-x)^L)/(sqrt(2*Pi*VAR)))
Integrating that from 0 to 1, we get a total value of .020. Remember that we still have to divide by the total sum of the weights to find the weighted average, but since that is just F(p), or the cumulative distribution function of the prior distribution, it is equal to one by definition. Therefore, P(B) = .02.
Finally, we have to calculate P(B|A). This is the probability of observing a 2-10 record, given that we are drawing a random team from the prior distribution that fulfills condition A, which is that the team has at least a .500 true W%. This is done very similarly to finding P(B) above, except we are only considering values of p>.5.
Start by calculating the same definite integral as before, but from .5 to 1 instead of from 0 to 1 (this is done by simply changing a textbox below the formula). This gives a value of .0045. That is the weighted sum of all the probabilities; to turn the weighted sum into an average, we still have to divide by the sum of all the weights, which in this case is .5 (this is the cdf F(p) from .5 to 1). Dividing .0045 by .5, we get .009. This is P(B|A).
P(A)=.5
P(B) = .02
P(B|A) = .009
P(A|B) = .009*.5/.02 = .22
The probability of a team that goes 2-10 being at least a true talent .500 team is about 22% (assuming our prior distribution is fairly accurate). As you can see, this is pretty far from what one might conclude from using the hypothesis test to reject the null hypothesis that the team is a .500 team. This is why it is important not to misconstrue the meaning of the hypothesis test. The hypothesis test only tells you a very specific thing, which is how likely or unlikely the observed result is if you assume the null hypothesis to be true. Rejecting the null hypothesis on this basis does not necessarily mean the null hypothesis is unlikely; that depends on the prior distribution of possible hypotheses that exist. Considering potential prior distributions allows us to make more relevant estimates and conclusions about the likelihood of the null hypothesis.
Another advantage of the Bayesian approach is that it gives us a full posterior distribution of possible results. For example, when we observe a 2-10 team, we can not only estimate the odds that it is a true .500 team, but also the odds that it is a true .550 team, or .600 team, or whatever. Also, since we have a full distribution of likelihoods, we can also figure out the expected value.
The posterior distribution of possible true talent W% for a team that is observed to go 2-10 is represented by the product we integrated earlier:
(((W+L)!/(W!*L!))*exp((-((x-u)^2))/(2*VAR))*(x^W*(1-x)^L)/(sqrt(2*Pi*VAR)))
We find the expected value of that function the same way we found the average value of the above probabilities. This time, we want to find the average value of x (or p, as we were calling it before), so we weight each value of x by the above function, and then divide by the sum of the weights. For the numerator, this means integrating the above function multiplied by x:
x * (((W+L)!/(W!*L!))*exp((-((x-u)^2))/(2*VAR))*(x^W*(1-x)^L)/(sqrt(2*Pi*VAR)))
The denominator is just the summation of the function not multiplied by x, which we already did above (it is the same thing as the P(B) above, or .020).
Plugging this into the definite integral calculator, we get:
0.009442586/0.020355243 = 0.464
So a team that goes 2-10 over 12 games will be, on average, about a .464 team (again, assuming our prior distribution is accurate).
As a shortcut for the above calculations, one can also use regression to the mean to estimate the expected value of the team's true W%. This is done by finding the point where random variance in the observed record equals the variance of talent in the population. We know the standard deviation of talent in the population, using our assumed prior, is .050 wins per game. The random variance in the observed record is n*p*(1-p), where n is the number of games and p is the teams' true W%. Since p mostly stays around .5, this approximately equal to n*.25 (it's actually about n*.2475, but the difference is minimal). When you have 100 observed games, the random variance will be 100*.25 = 25. The variance of talent will be (100*.05)^2 = 25. Therefore, after 100 games, the variance due to random variation will equal the variance of talent in the population.
At this point, we would regress exactly 50% to the mean to estimate the expected value of a team's true W%. This is the same as adding 100 games of league average performance to a team's observed record. This also works after any observed number of games. To estimate our 2-10 team's true W% with regression to the mean, we would add 50 wins and 50 losses to the observed record and get an expected W% of 52/112 = .464. How well regression to the mean approximates Bayesian probability depends on the prior distribution you choose, but in this case, it works very well (rounds to the same thousandths place).
This is all done assuming a prior that presumes nothing about the team in question other than the fact that it comes from a distribution of teams roughly like that we observe in MLB. What if, in addition to knowing the 2-10 team comes from MLB, we also know that the team employs several really good players and that we believe them to be one of the most talented teams in the league? We can adjust the prior for that information as well. Our prior distribution, after accounting for the amount of talent we believe to be on the team, might have a mean of .590 instead of .500. Let's say that we assume a normal distribution with a mean of .590 and a SD of .030 for our prior. Now we get an expected W%, after observing the team go 2-10, of .572. In this case, the absymal 12 game observed sample dropped our expectations for the team going forward from .590 to .572. Of course, this all depends on what prior you assume, but as long as you make reasonable assumptions, your estimate should give you a decent idea. Continue Reading...
Let's say that we have a hypothetical Major League team that has started the season 2-10. Say we want to see how likely it is that a team that goes 2-10 is still a .500 team. If you've taken any statistics courses, you may be familiar with hypothesis testing where you formulate a null hypothesis that the team is a .500 team, and then calculate the probability that they would go 2-10 by chance. You would then see that a .500 team will go 2-10 (or worse) over a 12 game span less than 2% of the time, and you'd probably reject your null hypothesis, depending on how high you set your significance level.
This does not, however, tell you anything about the likelihood that the team actually is a .500 team, only the likelihood that they would perform that badly if they were in fact a .500 team. To address the former issue, we can instead use a Bayesian approach.
To do that, we have to make an assumption about the population that the team is drawn from (in other words, about the spread of talent across all teams in the league). Most teams in MLB fall somewhere in the .400-.600 range (at least in true talent, if not in observed win percentage), so for convenience sake, let's just assume MLB teams follow a normal distribution of talent with a standard deviation of .050 W%.
This is our prior distribution. Once we have that, we can apply Bayes' Theorem:
P(A|B) = P(B|A)*P(A)/P(B)
We want to find the probability of A given B [P(A|B)], which is to say that we want to find the probability that a team drawn from our prior population distribution (u=.500, SD=.050) is actually a .500 (or better) team, given that we have observed that team to go 2-10 over 12 games. To do this, we need to find the probabilities P(B|A), P(A), and P(B).
P(A) is the simplest. This is the probability of a random team drawn from our prior distribution is at least a .500 team, ignoring of what we observed over the 12 game sample. This is just .500, because the population is centered around .500. So, P(A)=.5.
*NOTE-if you want to use a W% other than .500, all you have to do is find the probability of drawing a W% at least that high from the prior distribution, which is trivial when the prior distribution is normal since that is a common computer function. If you don't have a program that can calculate normal distribution probabilities, you can use an online tool.
P(B) is a bit more difficult. This is the probability that we observe a random team drawn from our prior distribution to go 2-10 over 12 games. This would be simple to calculate for any one team if we already know its true W%, but we need to know the average probability for all possible teams we could draw from our prior distribution. This will require a bit of calculus.
For any one team with a known true W% (p), the probability of going 2-10 is:
( 12! / (2! * 10!) ) * p^2 * (1-p)^10
where 12 represents the number of total games, 2 the number of wins, and 10 the number of losses. We need to find the average value of that formula across the entire prior distribution.
To do this, we utilize the same principle as a weighted average. In this case, the weight given to each possible value of p is represented by the probability density function of the prior distribution. So, for example, the odds of a .400 team going 2-10 are about 6.4%, and that 6.4% gets weighted by the quantity f(p), where f(p) is the pdf for our prior normal distribution. We repeat this for each possible value of p, add up the weighted terms, and then divide by the sum of the weights. As you have probably guessed, this means taking the definite integral (from p=0 to p=1) of the probabilities weighted by f(p):
INTEGRAL(f(p) * ( ( 12! / (2! * 10!) ) * p^2 * (1-p)^10 ) dp)
f(p) is just the normal distribution pdf, which is:
f(p) = e^((-((x-u)^2))/(2*VAR))/(sqrt(2*Pi*VAR)) ; u=.5, VAR=.05^2=.0025
As fun as it sounds to go ahead and do that by hand, we'll just let computers do this part for us too, using an online definite integral calculator. You can copy and paste this into the function field if you want to try it for yourself:
((12!/(2!*10!))*exp((-((x-.5)^2))/(2*.0025))*(x^2*(1-x)^10)/(sqrt(2*3.14159*.0025)))
or, more generally, if you want to play around with different records or different means and variances for the prior normal distribution:
(((W+L)!/(W!*L!))*exp((-((x-u)^2))/(2*VAR))*(x^W*(1-x)^L)/(sqrt(2*Pi*VAR)))
Integrating that from 0 to 1, we get a total value of .020. Remember that we still have to divide by the total sum of the weights to find the weighted average, but since that is just F(p), or the cumulative distribution function of the prior distribution, it is equal to one by definition. Therefore, P(B) = .02.
Finally, we have to calculate P(B|A). This is the probability of observing a 2-10 record, given that we are drawing a random team from the prior distribution that fulfills condition A, which is that the team has at least a .500 true W%. This is done very similarly to finding P(B) above, except we are only considering values of p>.5.
Start by calculating the same definite integral as before, but from .5 to 1 instead of from 0 to 1 (this is done by simply changing a textbox below the formula). This gives a value of .0045. That is the weighted sum of all the probabilities; to turn the weighted sum into an average, we still have to divide by the sum of all the weights, which in this case is .5 (this is the cdf F(p) from .5 to 1). Dividing .0045 by .5, we get .009. This is P(B|A).
P(A)=.5
P(B) = .02
P(B|A) = .009
P(A|B) = .009*.5/.02 = .22
The probability of a team that goes 2-10 being at least a true talent .500 team is about 22% (assuming our prior distribution is fairly accurate). As you can see, this is pretty far from what one might conclude from using the hypothesis test to reject the null hypothesis that the team is a .500 team. This is why it is important not to misconstrue the meaning of the hypothesis test. The hypothesis test only tells you a very specific thing, which is how likely or unlikely the observed result is if you assume the null hypothesis to be true. Rejecting the null hypothesis on this basis does not necessarily mean the null hypothesis is unlikely; that depends on the prior distribution of possible hypotheses that exist. Considering potential prior distributions allows us to make more relevant estimates and conclusions about the likelihood of the null hypothesis.
Another advantage of the Bayesian approach is that it gives us a full posterior distribution of possible results. For example, when we observe a 2-10 team, we can not only estimate the odds that it is a true .500 team, but also the odds that it is a true .550 team, or .600 team, or whatever. Also, since we have a full distribution of likelihoods, we can also figure out the expected value.
The posterior distribution of possible true talent W% for a team that is observed to go 2-10 is represented by the product we integrated earlier:
(((W+L)!/(W!*L!))*exp((-((x-u)^2))/(2*VAR))*(x^W*(1-x)^L)/(sqrt(2*Pi*VAR)))
We find the expected value of that function the same way we found the average value of the above probabilities. This time, we want to find the average value of x (or p, as we were calling it before), so we weight each value of x by the above function, and then divide by the sum of the weights. For the numerator, this means integrating the above function multiplied by x:
x * (((W+L)!/(W!*L!))*exp((-((x-u)^2))/(2*VAR))*(x^W*(1-x)^L)/(sqrt(2*Pi*VAR)))
The denominator is just the summation of the function not multiplied by x, which we already did above (it is the same thing as the P(B) above, or .020).
Plugging this into the definite integral calculator, we get:
0.009442586/0.020355243 = 0.464
So a team that goes 2-10 over 12 games will be, on average, about a .464 team (again, assuming our prior distribution is accurate).
As a shortcut for the above calculations, one can also use regression to the mean to estimate the expected value of the team's true W%. This is done by finding the point where random variance in the observed record equals the variance of talent in the population. We know the standard deviation of talent in the population, using our assumed prior, is .050 wins per game. The random variance in the observed record is n*p*(1-p), where n is the number of games and p is the teams' true W%. Since p mostly stays around .5, this approximately equal to n*.25 (it's actually about n*.2475, but the difference is minimal). When you have 100 observed games, the random variance will be 100*.25 = 25. The variance of talent will be (100*.05)^2 = 25. Therefore, after 100 games, the variance due to random variation will equal the variance of talent in the population.
At this point, we would regress exactly 50% to the mean to estimate the expected value of a team's true W%. This is the same as adding 100 games of league average performance to a team's observed record. This also works after any observed number of games. To estimate our 2-10 team's true W% with regression to the mean, we would add 50 wins and 50 losses to the observed record and get an expected W% of 52/112 = .464. How well regression to the mean approximates Bayesian probability depends on the prior distribution you choose, but in this case, it works very well (rounds to the same thousandths place).
This is all done assuming a prior that presumes nothing about the team in question other than the fact that it comes from a distribution of teams roughly like that we observe in MLB. What if, in addition to knowing the 2-10 team comes from MLB, we also know that the team employs several really good players and that we believe them to be one of the most talented teams in the league? We can adjust the prior for that information as well. Our prior distribution, after accounting for the amount of talent we believe to be on the team, might have a mean of .590 instead of .500. Let's say that we assume a normal distribution with a mean of .590 and a SD of .030 for our prior. Now we get an expected W%, after observing the team go 2-10, of .572. In this case, the absymal 12 game observed sample dropped our expectations for the team going forward from .590 to .572. Of course, this all depends on what prior you assume, but as long as you make reasonable assumptions, your estimate should give you a decent idea. Continue Reading...
Optimistic Projections.
UPDATE: The table in the article has been updated with actual 2011 wOBAs for each player, along with actual 2011 PAs. An aggregate line has been added with the combined projected and actual wOBAs weighted by actual 2011 PAs. Also, in light of Mike's response below regarding the handling of intentional walks in their projections, it is possible the RotoChamp wOBA values are artifically-inflated, so the difference between the average Roto projection and the actual might not be meaningful.
While looking through the projections posted at FanGraphs, I noticed that some of the RotoChamp projections seem a bit optimistic. For example, Jim Thome is projected with a .419 wOBA. Thome had a good year last year, putting up a .437 wOBA over 340 PA, but he's also 40 years old, and even with a potential HOF career behind him, his career wOBA is only .407.
This looks like a simple case of under-regressing 2010 performance and not enough weight given to past performance. However, other optimistic projections fall out of this pattern. For example, Albert Pujols is projected with a .449 wOBA, higher even than his career .434 mark despite Albert now being on the wrong side of 30 (it appears the wOBA projections may not remove IBB, so Albert's career wOBA with his IBBs counted as nIBBs would be .444; closer to his projection, but still lower). Albert's 2010 performance, however, does not seem to be driving the high projection; he hit only .420 last year.
Does RotoChamp see something important in projections like these, or is the optimism misplaced? I find 20 different players listed in both the Marcel and RotoChamp projections who are projected at least .030 points wOBA higher by RotoChamp than Marcel. They are:
This does not include prospects who have not appeared in the Majors, such as Brandon Belt, who RotoChamp likes a lot (.385 projected wOBA). Technically, Marcel projects these players with a league average wOBA, so they could be included, but whether or not RotoChamp's prospect insights add value is a separate issue than what I am looking at here. Other than Brandon Allen, these players all have fairly established Major League track records with plenty of data for a projection system to work with, and RotoChamp is still seeing them very differently from Marcel.
The test here is simple. At the end of the year, will Marcel's or RotoChamp's estimates for these 20 players be better? Additionally, will this group signicantly outperform its Marcel projections, even if they still end up closer to Marcel than RotoChamp? After all, RotoChamp could be finding something that Marcel is underselling in these players and still be over-weighting that insight to end up with overly optimistic projections.
Most of the players on the list are in their 30s or 40s (all except Miguel Cabrera, Jed Lowrie, and Brandon Allen). Their average age is 34. Many, like Thome, Jose Bautista, and Andruw Jones are coming off big 2010 seasons, while some, like Albert and Manny Ramirez, are big names projected for bigger numbers than their 2010s would indicate. Continue Reading...
While looking through the projections posted at FanGraphs, I noticed that some of the RotoChamp projections seem a bit optimistic. For example, Jim Thome is projected with a .419 wOBA. Thome had a good year last year, putting up a .437 wOBA over 340 PA, but he's also 40 years old, and even with a potential HOF career behind him, his career wOBA is only .407.
This looks like a simple case of under-regressing 2010 performance and not enough weight given to past performance. However, other optimistic projections fall out of this pattern. For example, Albert Pujols is projected with a .449 wOBA, higher even than his career .434 mark despite Albert now being on the wrong side of 30 (it appears the wOBA projections may not remove IBB, so Albert's career wOBA with his IBBs counted as nIBBs would be .444; closer to his projection, but still lower). Albert's 2010 performance, however, does not seem to be driving the high projection; he hit only .420 last year.
Does RotoChamp see something important in projections like these, or is the optimism misplaced? I find 20 different players listed in both the Marcel and RotoChamp projections who are projected at least .030 points wOBA higher by RotoChamp than Marcel. They are:
| Name | Age | Rel | Marcel | RotoChamp | diff | 2011 PA | 2011 wOBA |
| Jim Thome | 41 | 0.81 | 0.360 | 0.419 | 0.059 | 324 | 0.362 |
| Dan Johnson | 32 | 0.4 | 0.327 | 0.381 | 0.054 | 91 | 0.181 |
| Jose Bautista | 31 | 0.84 | 0.362 | 0.408 | 0.046 | 655 | 0.441 |
| Brandon Allen | 25 | 0.38 | 0.321 | 0.367 | 0.046 | 195 | 0.286 |
| Ramon Castro | 35 | 0.6 | 0.319 | 0.361 | 0.042 | 75 | 0.332 |
| Magglio Ordonez | 37 | 0.83 | 0.345 | 0.386 | 0.041 | 357 | 0.283 |
| Ryan Hanigan | 31 | 0.69 | 0.329 | 0.370 | 0.041 | 304 | 0.320 |
| Chipper Jones | 39 | 0.83 | 0.353 | 0.393 | 0.04 | 512 | 0.345 |
| Jorge Posada | 40 | 0.79 | 0.341 | 0.381 | 0.04 | 387 | 0.309 |
| Matt Diaz | 33 | 0.74 | 0.330 | 0.367 | 0.037 | 268 | 0.280 |
| Andruw Jones | 34 | 0.75 | 0.323 | 0.360 | 0.037 | 222 | 0.371 |
| Albert Pujols | 31 | 0.87 | 0.414 | 0.449 | 0.035 | 651 | 0.385 |
| David Ortiz | 36 | 0.85 | 0.347 | 0.382 | 0.035 | 605 | 0.405 |
| Jason Giambi | 40 | 0.78 | 0.326 | 0.359 | 0.033 | 152 | 0.407 |
| Matt Treanor | 35 | 0.64 | 0.279 | 0.312 | 0.033 | 242 | 0.291 |
| Miguel Cabrera | 28 | 0.87 | 0.390 | 0.422 | 0.032 | 688 | 0.436 |
| Chase Utley | 33 | 0.86 | 0.370 | 0.401 | 0.031 | 454 | 0.344 |
| Aubrey Huff | 35 | 0.87 | 0.345 | 0.376 | 0.031 | 579 | 0.294 |
| Jed Lowrie | 27 | 0.65 | 0.336 | 0.367 | 0.031 | 341 | 0.297 |
| Manny Ramirez | 39 | 0.81 | 0.371 | 0.401 | 0.03 | 17 | 0.052 |
| TOTAL PA | |||||||
| weighted average | 0.354 | 0.392 | 7119 | 0.353 | |||
This does not include prospects who have not appeared in the Majors, such as Brandon Belt, who RotoChamp likes a lot (.385 projected wOBA). Technically, Marcel projects these players with a league average wOBA, so they could be included, but whether or not RotoChamp's prospect insights add value is a separate issue than what I am looking at here. Other than Brandon Allen, these players all have fairly established Major League track records with plenty of data for a projection system to work with, and RotoChamp is still seeing them very differently from Marcel.
The test here is simple. At the end of the year, will Marcel's or RotoChamp's estimates for these 20 players be better? Additionally, will this group signicantly outperform its Marcel projections, even if they still end up closer to Marcel than RotoChamp? After all, RotoChamp could be finding something that Marcel is underselling in these players and still be over-weighting that insight to end up with overly optimistic projections.
Most of the players on the list are in their 30s or 40s (all except Miguel Cabrera, Jed Lowrie, and Brandon Allen). Their average age is 34. Many, like Thome, Jose Bautista, and Andruw Jones are coming off big 2010 seasons, while some, like Albert and Manny Ramirez, are big names projected for bigger numbers than their 2010s would indicate. Continue Reading...